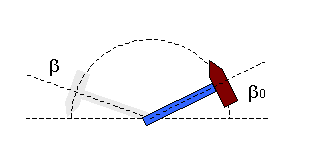
A diagram of the situation is shown below:

This does not show how the axe is powered. β 0 in the diagram is the starting angle of the axe, and β is the angle though which the axe has traversed. In this page we will derive equations which describe how this angle relates to the rotational speed of the axe at any point, the kinetic energy which the axe has, and the time taken to get to any point. This calculation does not take gravity into account, which in the situation pictured above will slow down the axe slightly until it reaches an upright position, and speed up the axe in the second part of its journey to the final position shown uncoloured. The effect of gravity should be negligable anyway as long as the motor is powerful enough and the axe not very heavy.
The calculations are performed for an axe driven by a DC electric motor, and by a pneumatic piston.

In this equation, ω1 is the no-load speed of the motor, T1 is the stall torque of the motor, and I is the moment of inertia of the weapon. To find out the moment of inertia of the weapon, refer to the table of moment of inertia equations here. Proofs of these equations are presented here if you are interested.
The second gives us the angle the axe has reached after a time, t:
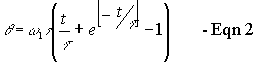
Since this second equation cannot be rearranged easily, instead, it is easier to find the inverse value by plotting the graph and looking up the value of t for a given angle. The graph shown assumes the following values:
Motor no-load speed, ω1 = 314 rad/s
(=3000 rpm)
Motor stall torque, T1= 10 Nm
Total moment of inertia, I = 0.02 N/m
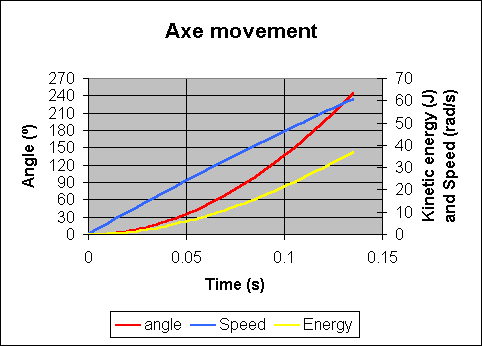
The spreadsheet for drawing this graph in Microsoft Excel '97 format is included here.
Using the graph, we can see that the axe will get to the 180 degrees in about 115 milliseconds. We can now use equation 1 or look on the graph to determine the speed of the axe at this time, Ω = 52.5 radians per second. The energy in the axe is given by the equation
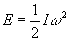
which in this case is 28 Joules.
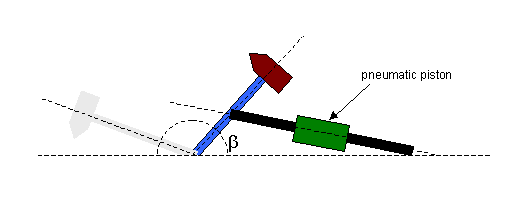
This has been simplified so the dimensions and angles can all be labelled below:
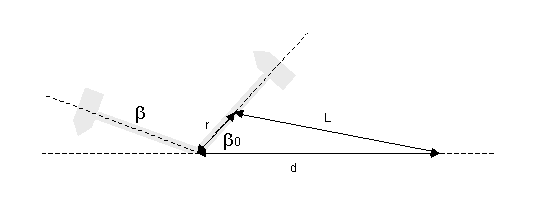
In this diagram, β0 is the starting position of the axe, and β is the current position. We would like to derive equations for the energy, speed and time to get to that point for any angle β. Again, this turns out to be extremely difficult to do. If you want to see the maths, look here. Instead, we use an iterative approach in an Excel spreadsheet for pneumatically driven axes by summing all Δt up to the angle in question. The Δt for each angle is the difference in angle from the last line (always 1 degree) divided by the speed at that angle, as defined in equation 8.
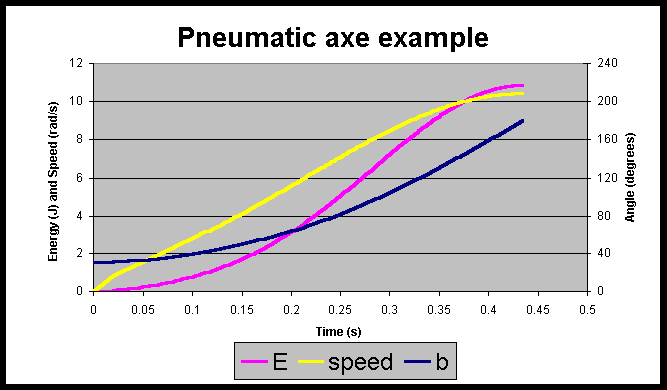
Using the spreadsheet, with the parameter values the same as previously, the following graph is produced:
Links
[E5] An excellent tutorial all about axe weapons powered by pneumatics. If
you can convert the American units (pounds, feet, and slugs!) which he
cheekily calls 'English units', then there's a lot of useful information in
there.
http://www.planethalflife.com/hlwf/ax1.html