
This uses the result derived in the calculation for the spin-up equations of a spinning disk weapon using a permanent magnet motor. That resulted in an equation for the rotational speed of the disk of:

In this equation, ω1 is the no-load speed of the motor, T1 is the stall torque of the motor, and I is the moment of inertia of the weapon. To find out the moment of inertia of the weapon, refer to the table of moment of inertia equations here. Proofs of these equations are presented here if you are interested.
Since the rotational speed is the differential of the rotated angle, i.e.
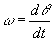
then
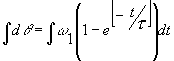
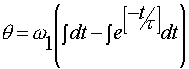
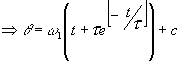
Now we have an equation which gives us the angle that the axe has travelled through after a time t. The ‘c’ in the equation is a constant of integration, which must have the value c = -τω1 so that the angle is zero when t is zero.
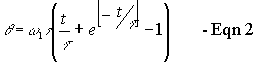
Rearrangement of equation 2 will give us the time taken for the axe to reach an angle θe where we are assuming it will be hitting the opponent. However, this equation is extremely difficult to rearrange in terms of ‘t’. Mathematica online gives us the following solution:

ProductLog is a rather complex mathematical function, which can be approximated to a series function, which to the fifth order is given by:
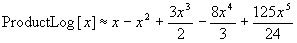
This is a very difficult equation to use as it is, and so will not be taken any further.