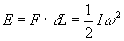(Eqn 1)
By far the easiest way to calculate the energy is to use the conservation of energy law, which states that energy can be neither created or destroyed. That means that the energy imparted into the axe by the pneumatic piston must all be placed into the kinetic energy of the system. All this kinetic energy will then be imparted into the opponent when the axe hits it.
The energy imparted by the piston is simply the force on the piston times the distance it travels. The kinetic energy of the rotating axe is half its moment of inertia times its rotational velocity squared. Thus:
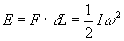(Eqn 1)
where ΔL is the change in length of the side of the triangle L as the piston expands.
Therefore we can write a term for the rotational speed given a change in L:
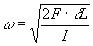(Eqn 2)
How does this relate to the angle β shown in the diagram? This can be solved using the cosine rule for triangles, which gives us:
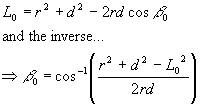(Eqn 3,4)
Since the values that we want to design with are really the start angle, which is where the axe rests on the robot, and the end angle, which is the predicted angle when the axe hits the opponent, we would like equations for energy and speed in terms of β0 and β1.
Therefore ΔL can be written as:
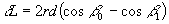(Eqn 5)
Plugging the definition for ΔL into the equations of energy and speed gives:
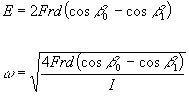(Eqn 6,7)
Now we just need to derive an equation for the time taken to get from the start angel β0 to the end angle β1. We have equations to draw a graph of the speed of the axe against the angle it is at. The graph below uses the following parameter values:
Starting angle β = 30º
Piston force, F = 30N
r = 0.2m
d = 0.6m
L0 = 0.438m
Moment of inertia, I = 0.2N/m
The time taken to get to an angle β can be calculated as follows. Referring to the graph above, the time taken for the angle to progress through the δβ angle shown is the angle divided by the rotational speed at that point, i.e.
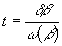(Eqn 8)
as the small angle δβ tends towards an infinitely small angle
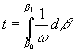(Eqn 9)
Ω has already been defined in terms of angle
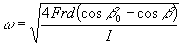
so
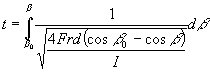
Using Wolfram Mathematica Integrator online to solve this equation results in
(Eqn 12)
The EllipticF function is a very complex function (described here if you are interested) In conclusion, deriving an equation to give us the time at a point β is not very fruitful.