Making Sense of Sense Resistors


1. Temperature Effects


by Dennis Feucht

Some components are relatively unimportant in their effect on overall circuit behavior. Sense resistors are not one of them. It may only be a resistor, but it's a very important resistor with subtleties that can impede design progress.

Temperature Coefficient
Sense resistors are usually power resistors in that they dissipate non-negligible amounts of power and are typically rated at 0.5 to 5 W. At the same time, they must hold their resistance value, for it contributes proportionally to the current measurement. Temperature coefficient (TC) of resistance is consequently of high design importance. Using a clipped length of copper wire will demonstrate this point. In a motor drive, the torque will fall off as the motor operates due to the increasing resistance of the copper sense resistor, as it heats. Wire made of alloys with low TCs are available for use instead.

But sometimes a copper sense resistor, whether as a discrete wire resistor or a circuit-board trace, can be used to advantage. The TC of copper is fairly constant over a wide temperature range, and its positive TC of about +0.4 %/°C can be used to compensate for the characteristically negative TC (–2.2 mV/°C) of a semiconductor junction elsewhere in the current control loop.

Actual Sense Resistors
One simple approach to sense resistors is to make your own out of a low TC conductive material. Manganin wire, an alloy of copper, manganese, and nickel, has a low TC of within  15 ppm/°C from 0 to 80 °C. AWG # 18 manganin wire has a resistivity of 0.361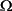/m. Smaller diameters are available and the wire can be bought by the roll. Cut the wire to length for the desired resistance, tin the ends, and solder into the board. A manganin resistor is shown in Figure 1 (left). By keeping the half-loop area small, inductance is minimized. The one shown has a resistance of 25 m.


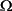Figure 1: Homemade and Commercial Sense Resistors

If you do not want to make your own, the resistors shown on the right on Figure 1 (front and rear) are commercially available power resistors made of a low-TC metal foil on an anodized aluminum substrate, and in TO-220 or TO-247 packages. Several companies, such as Caddock Electronics, now supply these accurate, low TC, power resistors at an attractive price for power-circuit design.

Another commonly-used low-TC material is nickel-chromium, or nichrome. Its resistivity of 133 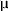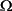-cm requires less wire length than mangagin's 43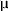 -cm, which can reduce inductance for very low-value resistors. Manganin, however, is superior to nichrome in TC and long-term stability of resistance value.

If future circuit-board fabrication technology allows a wider range of substrate materials (more than copper), thin-film power resistors can be integrated onto the board during layout. With clever circuit design, even copper traces can be TC-compensated with BJT junctions.

Kelvin Sensing Resistors
Series parasitic resistance is also a nuisance for low-value resistors. It is necessary to sense across the actual resistance of specified value and not some of the component lead resistance in addition. To solve this problem, 4-wire, or Kelvin, sensing is made possible with 4-wire resistors, such as those shown on Figure 2. The leads are attached internally to the desired resistance and are brought out of the package in pairs.

Figure 2
Figure 2: Kelvin Sensing Resistors

Kelvin-sensing resistors are also available in foil-on-substrate form, as shown on Figure 3. (The quarter is for size comparison.) The smaller, inner leads are 4-wire Kelvin sense leads while the wider, outer leads are the drive leads.

Figure 3
Figure 3: Kelvin-sensing Resistors
in foil-on-substrate form

Closure
Current-sense resistors for power electronics must be of low TC, relatively high power rating, and accurate at low resistance values. Such resistors are commercially available, in multiple packages, and at moderate prices. If prices are too high for a given application, consider making instead of buying sense resistors out of manganin wire, or for the lowest cost, use a copper circuit-board trace compensated by a silicon junction.


2. Parasitic Series Inductance—Frequency Sweep Measurement

A sense resistor is not only a resistor. A better model includes series inductance. The terminal leads (or terminal traces for surface-mount resistors) contribute an inductive element. In most resistor applications, this inductance is of no consequence, for it forms a time constant that is very small. But when the resistance is also small, the time constant, τ = L/R, becomes large enough so that the frequency 1/τ lies too close to the loop bandwidth of the power circuit.

It is not difficult to encounter parasitic inductances in the 50 nH to 200 nH range. This is too small a value to measure accurately on common RLC meters (or "bridges"), but can be measured conveniently on the lab bench by different methods (covered below). A 100 mΩ sense resistor with a series inductance of 100 nH has a time constant of 1 µs. And a 10 mΩ resistor will have a time constant of 10 µs, or a break frequency of about 16 kHz, within the bandwidth of many power-circuit feedback loops.

The series RL combination has an impedance of

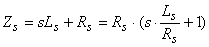where s = jΩ for frequency-response analysis (and Ω = 2πf, where f is the frequency in Hertz). The additional zero at a radian frequency of 1/(Ls/Rs) introduces an additional pole in a current-amplifier feedback loop if it is in the feedback path. Consequently, the zero cannot be ignored, and some estimate of the parasitic inductance becomes worthwhile.

Parasitic Inductance Measurement: Frequency Sweep Method
We will examine two possible methods to measure series inductance based on the frequency and time domains, in that order.

The test circuit shown below can be built easily on a lab bench and used to measure the parasitic series inductance. Typical function generators have 50 Ω outputs and can be used for this measurement.

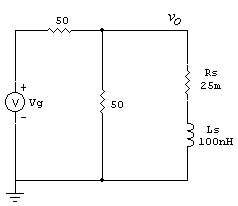
Figure 1
Figure 1 - Test Circuit Used to Measure the Parasitic Series Inductance

Let the generator source resistance and its output terminating resistance (both 50 Ω) be combined (in parallel) to form the equivalent series source resistance of Rg = 25 Ω. The transfer function of this circuit is

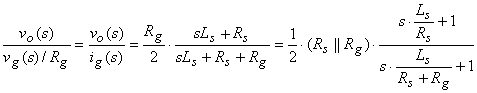For Rg >> Rs, this is approximated by

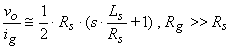By frequency-sweeping the generator, the frequency fa at which the amplitude increases by a times is then substituted into

to produce the value of Ls. (Use a value of a >> 1 to avoid the knee of the frequency-response curve around the break frequency.) For a = 5, sweep the generator upward in frequency until the measured amplitude is 5 times that of its unchanging, low-frequency value. Then substitute a and this frequency, fa, into the above equation for Ls.

Several factors that limit the usefulness of this method are listed below.

  1. Resistance (distinct from reactance) increases with frequency due to the skin effect, the self-induced eddy-current effect within a conductor. Resistance increases above a frequency at which the effective depth of current penetration into the conductive material is reduced. Thin-film resistors suffer this effect at relatively higher frequencies than bulk resistors because the skin depth exceeds their thin conductive dimension at lower frequencies, causing no change in their effective resistance.
  2. The source cable, if not terminated into 50 Ω, will set up standing waves, which degrade the accuracy of the amplitude measurement. If possible, set up the test at the generator output terminals as shown below, but preferably not with a ×10 scope probe, as shown.

    Figure 2
    Figure 2 - Recommended Setup of Function Generator Output

    The better approach is to use a 50 Ω terminated cable, as shown in Figure 3. Even better, especially for chip resistors, is to use a GR line insertion unit to preserve the 50 Ω cable environment.

    Figure 3
    Figure 3 - Use of 50 Ω Terminated Cable with Function Generator


3. Parasitic Series Inductance—Pulse Response Measurement

Parasitic Inductance Measurement: Pulse Response Method
A better series-inductance measurement technique uses a pulse generator. In the time domain, Rs can be eliminated from its effect on the measurement, a big advantage over the previous approach. Using the same setup as before, except with a pulse generator as an open source, the generator voltage pulse rising transition is adjusted to be 10 V in 50 ns, or 200 V/µs in this case. Then the source — still considered to be a current source (because Rg >> Rs) — drives the sense resistor with a current ramp of

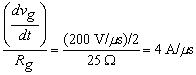(The ÷ 2 is due to the 50 Ω termination divider.) The inductance follows from the v-i relationship for inductance:

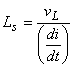    Equation 2 ,

where vL is the constant inductor voltage due to the current ramp.

The following waveforms were observed with the inductance driven by a Tektronix PG508 pulse generator.

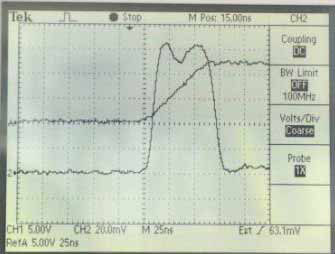
Figure 1
Figure 1

The top waveform (A) is the open-source voltage without a sense resistor; the ch 2 waveform is the response with a resistor, though only approximately time-aligned with the (stored) A waveform. (Note the ×1 setting for ch 2, which is terminated with 50 Ω.)

The voltage, vo, steps up to vL, a value of about 100 mV (on ch 2, at 20 mV/div). The current-ramp voltage drop across Rs causes a ramp-up superimposed on vL, which is negligible and undiscernible amidst waveform ringing. The pulse flattens on top to a constant voltage, leaving (on ch 2) a constant-current drive of Rs, producing about 6 mV (about Ľ div). The value of Rs can be calculated from the voltage-divider formula, where Vg (= 12.5 V) drives Rg = 25 Ω in series with Rs to produce about 6 mV across it:

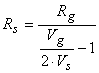    Equation 3 .

For this measurement, the resulting value of Rs is about 24 mΩ, which is 4% less than the approximately 25 mΩ measured with an RLC meter.

The inductance is calculated from the measured voltage:

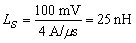    Equation 4 ,

which is a reasonable value based on the geometry.

Several factors that limit the usefulness of this method are listed below.

Closure
It is difficult to measure the series inductance of small-value resistors. An approximate value can be measured, however, using a very simple setup with a pulse generator and an oscilloscope. This approach will yield the small values not measurable with most RLC meters. A network analyzer can provide more accurate measurements at a much higher price.

Copyright © Dennis L. Feucht, 2000


4. Example problem

Question:

We are looking for the following shunt resistors.

    Current
    (A)    		 Voltage Drop
    (mV)    		 TCR
    (ppm)
    40 100 10
    1 100 10

Can you kindly suggest a manufacturer?

Answer:

Current sense resistors are sometimes called shunt resistors. While many people think of a shunt as "a piece of wire with low resistance," there are actually a number of considerations.

Small Values—First, a current sense resistor must be large enough so that a reasonable voltage drop develops across it. On the other hand, the resistance must be kept small, otherwise it dissipates too much power. To obtain low resistance values, one has to use special metal alloys. Commercially, one can purchase current shunt/sense resistors with values in the range 0.0003–100 Ω, designed for currents in the range 1–30,000 A.

Temperature Coefficient of Resistance (TCR)—Clearly the questioner is concerned how the shunt resistance will change with temperature, since this will directly impact the accuracy of any measurements made. A quick examination of manufacturer's catalogs show that typical TCRs of current shunt/sense resistors are in the range 100–700 ppm/°C, or equivalently, 0.01–0.07%/°C. A TCR of 10 ppm/°C (0.001%/°C) is a stringent requirement by any measure. Most pure metals have much higher TCRs, but there are a few alloys such as Manganin that have TCRs below 20 ppm/°C.

Inductance—If the shunt will be used to measure AC current, then inductance may become an issue. Normally, one could safely ignore the inductance of a piece of wire 0.5–1.0 inch long, even at relatively low frequencies. However, since shunt/current sense resistors have values in the milliohm range, even inductances in the order of 100 nH can affect measurements. ChipCenter's Dennis Feucht explored the inductance of shunt/sense resistors in a series of articles (see the References below).

Thermal EMV—A current shunt/sense resistor normally implies at least three different metals:

    (a) copper wire or PCB cladding,
    (b) lead/tin solder, and
    (c) the special low TCR alloy of the current shunt/sense resistor.

Whenever dissimilar metals are in contact, it is almost inevitable that small EMVs are generated. This will be in the range of ± 2 µV/°C for the metal-metal junction in current shunt/sense resistors.

Returning to the question, the table below shows that the questioner wants:

    (a) 2.5 mΩ, 4 W, and
    (b) 100 mΩ, 0.1 W resistors.

    Current
    (A)    		 Voltage Drop
    (mV)    		 TCR
    (ppm)    		 Resistance
    (mΩ)    		 Power
    (W)
    40 100 10 2.5 4
    1 100 10 100 0.1

It is not clear whether inductance is an issue.

One possibility would be the A-H type of current-sense resistors from Istotek that are available in resistances of 0.001–100 Ω, are made from Manganin foil with low (< 10 ppm) TCR, and are rated at 10 W. Isotek offers online ordering as well. I list a few other suppliers in the references below.

References

  1. Caddock manufacturers a diverse range of precision resistors, including current-sense resistors.

  2. Dennis Feucht, Making Sense of Sense Resistors — Part 1: Temperature Effects, ChipCenter.

  3. Dennis Feucht, Making Sense of Sense Resistors — Part 2: Parasitic Series Inductance–Frequency Sweep Measurement, ChipCenter.

  4. Dennis Feucht, Making Sense of Sense Resistors — Part 3: Parasitic Series Inductance–Pulse Response Measurement, ChipCenter.

  5. Empro Manufacturing Company markets a wide range of Manganin (remember: TCR for Manganin ~ 20 ppm/°C) DC current shunts.

  6. Isotek Corporation markets specialized resistors, including current-sense resistors.

  7. Ohmite is a well-known manufacturer of a wide variety of resistors. Some of their resistors may be used for current sensing applications.

  8. There are laboratory test-equipment current shunts available, where the user programs a resistance value in.
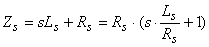
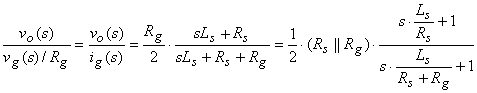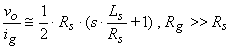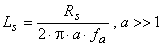
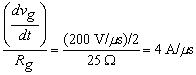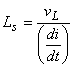
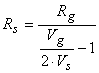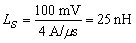